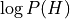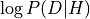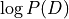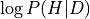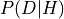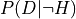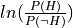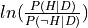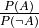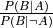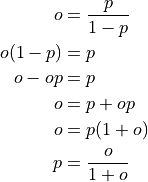cardinal_pythonlib.probability
Original code copyright (C) 2009-2022 Rudolf Cardinal (rudolf@pobox.com).
This file is part of cardinal_pythonlib.
Licensed under the Apache License, Version 2.0 (the “License”); you may not use this file except in compliance with the License. You may obtain a copy of the License at
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an “AS IS” BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
Miscellaneous probability functions.
- cardinal_pythonlib.probability.bayes_posterior(prior: float, likelihood: float, marginal_likelihood: float) float[source]
Returns P(H | D), the posterior probability of hypothesis H, given data D.
- Parameters:
- Returns:
P(H | D), the probability of H given D.
- Return type:
float
Bayes’ rule:
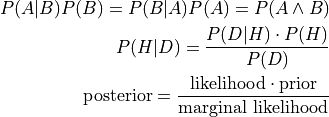
- cardinal_pythonlib.probability.ln(x: float) float[source]
Version of
math.log()that treats log(0) as-inf, rather than crashing withValueError: math domain error.- Parameters:
x¶ – parameter
- Returns:
ln(x), the natural logarithm of x
- Return type:
float
See https://stackoverflow.com/questions/42980201/logarithm-of-zero-in-python.
For speed, use
from math import log as math_log, etc.:Note also that although floats can’t be “too close to zero” to cause an error, other things (like Decimal objects) can. See https://stackoverflow.com/questions/19095774/python-math-domain-errors-in-math-log-function
Exception catching is likely faster:
- cardinal_pythonlib.probability.log10(x: float) float[source]
Version of
math.log10()that treats log(0) as-inf, rather than crashing withValueError: math domain error.- Parameters:
x¶ – parameter
- Returns:
log10(x), the logarithm to base 10 of x
- Return type:
float
See https://stackoverflow.com/questions/42980201/logarithm-of-zero-in-python.
- cardinal_pythonlib.probability.log_bayes_posterior(log_prior: float, log_likelihood: float, log_marginal_likelihood: float) float[source]
Exactly equivalent to
bayes_posterior(), but using log probability.
- cardinal_pythonlib.probability.log_likelihood_ratio_from_p(p_d_given_h: float, p_d_given_not_h: float) float[source]
Returns
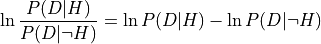
- cardinal_pythonlib.probability.log_odds_from_1_in_n(n: float) float[source]
If the chance of something occurring are 1 in n, then its probability is
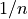 , and its odds are
, and its odds are 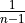 . This function
returns the log of those odds.
. This function
returns the log of those odds.- Parameters:
n¶ –
n, as above- Returns:
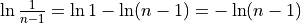
- Return type:
float
- cardinal_pythonlib.probability.log_odds_from_probability(p: float) float[source]
Returns log odds from a probability.
- Parameters:
p¶ – probability
- Returns:
ln(odds)
- Return type:
float
See
- cardinal_pythonlib.probability.log_posterior_odds(log_prior_odds: float, log_likelihood_ratio: float) float[source]
Exactly as for
posterior_odds(), but with log odds.
- cardinal_pythonlib.probability.log_posterior_odds_from_bool_d_pdh_pdnh(log_prior_odds: float, d: bool, p_d_given_h: float, p_d_given_not_h: float) float[source]
Calculates posterior odds.
- cardinal_pythonlib.probability.log_posterior_odds_from_pdh_pdnh(log_prior_odds: float, p_d_given_h: float, p_d_given_not_h: float) float[source]
Calculates posterior odds.
- cardinal_pythonlib.probability.log_probability_from_log_odds(log_odds: float) float[source]
No obvious quick form for this:
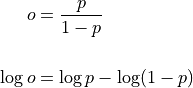
- Parameters:
log_odds¶ – ln(o); natural log of o
- Returns:
ln(p)
- Return type:
float
- cardinal_pythonlib.probability.odds_from_probability(p: float) float[source]
Returns odds, given a probability.
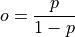
- Parameters:
p¶ – probability
- Returns:
odds
- Return type:
float
- cardinal_pythonlib.probability.posterior_odds(prior_odds: float, likelihood_ratio: float) float[source]
Returns the posterior odds for a hypothesis, given the prior odds and the likelihood ratio.
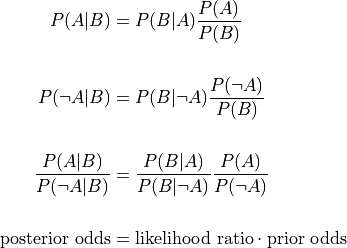
- Parameters:
- Returns:
posterior odds,
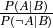
- Return type:
float
- cardinal_pythonlib.probability.probability_from_log_odds(log_odds: float) float[source]
Returns a probability from a log odds.
- Parameters:
log_odds¶ – ln(o); natural log of o
- Returns:
p
- Return type:
float