cardinal_pythonlib.maths_numpy
Original code copyright (C) 2009-2022 Rudolf Cardinal (rudolf@pobox.com).
This file is part of cardinal_pythonlib.
Licensed under the Apache License, Version 2.0 (the “License”); you may not use this file except in compliance with the License. You may obtain a copy of the License at
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an “AS IS” BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
Miscellaneous mathematical functions that use Numpy (which can be slow to load).
- cardinal_pythonlib.maths_numpy.inv_logistic(y: float | ndarray, k: float, theta: float) float | None[source]
Inverse standard logistic function:
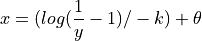
- cardinal_pythonlib.maths_numpy.logistic(x: float | ndarray, k: float, theta: float) float | None[source]
Standard logistic function.
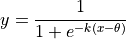
- cardinal_pythonlib.maths_numpy.pick_from_probabilities(probabilities: List[float] | ndarray) int[source]
Given a list of probabilities like
[0.1, 0.3, 0.6], returns the index of the probabilistically chosen item. In this example, we would return0with probability 0.1;1with probability 0.3; and2with probability 0.6.- Parameters:
probabilities¶ – list of probabilities, which should sum to 1
- Returns:
the index of the chosen option
- Raises:
ValueError –
than or equal to the cumulative sum of the supplied probabilities (i.e. –
if you've specified probabilities adding up to less than 1) –
Does not object if you supply e.g.
[1, 1, 1]; it’ll always pick the first in this example.
- cardinal_pythonlib.maths_numpy.softmax(x: ndarray, b: float = 1.0) ndarray[source]
Standard softmax function:
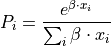
- Parameters:
- Returns:
vector of probabilities corresponding to the input values
where:
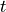 is temperature (towards infinity: all actions equally likely;
towards zero: probability of action with highest value tends to 1)
is temperature (towards infinity: all actions equally likely;
towards zero: probability of action with highest value tends to 1)Temperature is not used directly as optimizers may take it to zero, giving an infinity; use inverse temperature instead.
[Daw2009] Daw ND, “Trial-by-trial data analysis using computational methods”, 2009/2011; in “Decision Making, Affect, and Learning: Attention and Performance XXIII”; Delgado MR, Phelps EA, Robbins TW (eds), Oxford University Press.
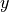
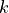
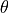
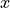
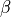 , or inverse temperature
[Daw2009], or
, or inverse temperature
[Daw2009], or 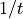 ; see below
; see below